Grammaire L-attribuée
Dans le monde d'aujourd'hui, Grammaire L-attribuée est devenu un sujet d'intérêt général. De son impact sur la société à sa pertinence dans le domaine professionnel, Grammaire L-attribuée a capté l'attention de personnes de tous âges et de toutes cultures. Avec d’innombrables opinions et perspectives autour de Grammaire L-attribuée, il est crucial d’analyser en profondeur ses implications et ses conséquences. Dans cet article, nous explorerons divers aspects liés à Grammaire L-attribuée, dans le but de fournir un aperçu large et complet de ce sujet. De son origine à ses possibles évolutions futures, nous examinerons Grammaire L-attribuée sous différents angles pour comprendre son importance aujourd’hui.
Une grammaire L-attribuée est un type spécial de grammaire attribuée qui permet aux attributs d'être évalués dans une traversée de gauche à droite de l'arbre syntaxique. Cela permet à l'évaluation des attributs d'être facilement incorporée dans une analyse descendante.
De nombreux langages de programmation sont L-attribués. Un type spécial de compilateur, les compilateurs étroits, sont fondés sur certaines formes de grammaires L-attribuées.
Généralités
Dans les productions d'une grammaire L-attribuée, les attributs d'un symbole syntaxique peuvent dépendre de ceux des symboles qui les précèdent dans la production syntaxique (que ce soit en membre gauche ou droit)
Exemple
A → A1 A2…An L'attribut de A2 dépend de ceux de A1 et A. L'attribut de An dépend de ceux de An-1… A1 et A.
Définitions
Une grammaire est dite L-attribuée si, dans toute règle A → X1 X2 ... Xn, le calcul dans l'action associée d'un attribut Xi.b ne dépend que des attributs des symboles X1 X2 ... Xi-1 et des attributs hérités de A.
Un attribut est soit :
- hérité : il participe au calcul de la valeur d’attributs des nœuds fils. C'est-à-dire du nœud vers les fils.
- synthétisé : participe au calcul de la valeur d’attributs du nœud père.
Algorithme de Parcours
parcours(nœud n) {
pour chaque fils m de n {
calculer les attributs hérités de m ;
parcours(m) ; }
calculer les attributs synthétisés de n ; }
Flot possible
le parcours d'un arbre syntaxique dans une grammaire L-attribuée se fait par la recherche en profondeur.
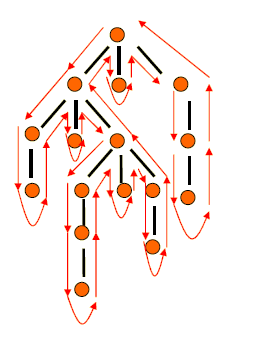
Graphe de dépendances
Dans le graphe de dépendances d’attributs d'une grammaire L-attribuée, les nœuds sont visités en profondeur : visiter le nœud courant, ensuite les fils de gauche à droite en profondeur.
Conséquences : dans une production A → A1 A2 … An, le calcul d'un attribut d’un symbole αi à Ai associé ne doit pas nécessiter celui d'un symbole se trouvant à sa droite, que ce soit dans la production courante ou dans toutes les dérivations possibles.
Évaluation ascendante
Une évaluation ascendante construit l'arbre syntaxique de bas en haut. Une grammaire L-attribuée requiert le parcours de l'arbre de haut en bas.
À priori, il semble impossible de faire cohabiter l'évaluation ascendante avec une grammaire L-attribuée. Et pourtant…!
Évaluation descendante
On met les routines entre les symboles syntaxiques L'analyse descendante reconnaît les symboles de gauche à droite, et exécute ainsi les routines de gauche à droite.

A → R0 α1 R1 α2 R2…An Rn
Les attributs calculés par la routine Ri ne doivent dépendre que des attributs calculés par les routines exécutées avant Ri. Le problème qui se pose Pour l'analyse descendante est l’élimination de la récursivité à gauche.
Élimination de la récursivité à gauche
Principe
Grammaire résultante L-attribuée, sous forme de schéma de traduction, se fait par l'introduction de nouvelles variables
- A → AY {A.a := g(A1.a, Y.y)}
- A → X {A.a := f(X.x)}
Devient :
- A → X {R.he := f(X.x)}
- R {A.a := R.s}
- R → Y {R1.he := g(R.he, Y.y)}
- R {R.s := R1.s}
- R → {R.s := R.he}
Exemple
- E → E +T {E.val := E1.val + T.val}
- E → E –T {E.val := E1.val – T.val}
- E → T {E.val := T.val}
- T → (E ) {T.val:= E.val}
- T → n {T.val := n.val}
Devient :
- E → T {R.he := T.val}
- R {E.val := R.s}
- R → +T {R1.he := R.he + T.val}
- R {R.s := R1.s}
- R → –T {R1.he := R.he – T.val}
- R {R.s := R1.s}
- R → {R.s := R.he}
- T → (E ) {T.val:= E.val}
- T → n {T.val := n.val}
Liens externes
- (fr) http://www.dicosmo.org/CourseNotes/Compilation/0304/Cours07/notes-4.pdf : document PDF en ligne
- (fr) http://www.fil.univ-lille1.fr/~nebut/portail/compilS5/fichiers/cours/anSem/cours1.pdf : document PDF en ligne