Injection (mathématiques)

Apparence déplacer vers la barre latérale masquer

Une application f est dite injective ou est une injection si tout élément de son ensemble d'arrivée a au plus un antécédent par f, ce qui revient à dire que deux éléments distincts de son ensemble de départ ne peuvent pas avoir la même image par f.

Lorsque les ensembles de départ et d'arrivée de f sont tous les deux égaux à la droite réelle ℝ, f est injective si et seulement si son graphe intersecte toute droite horizontale en au plus un point.

Si une application injective est aussi surjective, elle est dite bijective.

Définition formelle

Représentation graphique de la notion d'injection : pour tout y {\displaystyle y}

y

de Y {\displaystyle Y}

Y

, il existe au plus un x {\displaystyle x}

x

de X {\displaystyle X}

X

tel que y = f ( x ) {\displaystyle y=f(x)}

y=f(x)

Une application f : X → Y {\displaystyle f:X\to Y} $f:X\to Y$ est injective si pour tout y ∈ Y {\displaystyle y\in Y} $y\in Y$ , il existe au plus un x ∈ X {\displaystyle x\in X} $x\in X$ tel que f ( x ) = y {\displaystyle f(x)=y} $f(x)=y$ , ce qui s'écrit :

∀ ( x , x ′ ) ∈ X 2 , ( f ( x ) = f ( x ′ ) ⇒ x = x ′ ) {\displaystyle \forall (x,x')\in X^{2},(f(x)=f(x')\Rightarrow x=x')}

\forall (x,x')\in X^{2},(f(x)=f(x')\Rightarrow x=x')

L'implication précédente équivaut à sa contraposée :

∀ ( x , x ′ ) ∈ X 2 , ( x ≠ x ′ ⇒ f ( x ) ≠ f ( x ′ ) ) {\displaystyle \forall (x,x')\in X^{2},(x\neq x'\Rightarrow f(x)\neq f(x'))}

\forall (x,x')\in X^{2},(x\neq x'\Rightarrow f(x)\neq f(x'))

Exemple concret

Prenons le cas d'une station de vacances où un groupe de touristes doit être logé dans un hôtel. Chaque façon de répartir ces touristes dans les chambres de l'hôtel peut être représentée par une application de l'ensemble des touristes, X, vers l'ensemble des chambres, Y (à chaque touriste est associée une chambre).

L'hôtelier souhaite que l'application soit surjective, c'est-à-dire que chaque chambre soit occupée. Cela n'est possible que s'il y a au moins autant de touristes que de chambres.
Les touristes souhaitent que l'application soit injective, c'est-à-dire que chacun d'entre eux ait une chambre individuelle. Cela n'est possible que si le nombre de touristes ne dépasse pas le nombre de chambres.
Ces contraintes ne sont compatibles que si le nombre de touristes est égal au nombre de chambres. Dans ce cas, il sera possible de répartir les touristes de telle sorte qu'il y en ait un seul par chambre, et que toutes les chambres soient occupées : l'application sera alors à la fois injective et surjective ; on dira qu'elle est bijective.

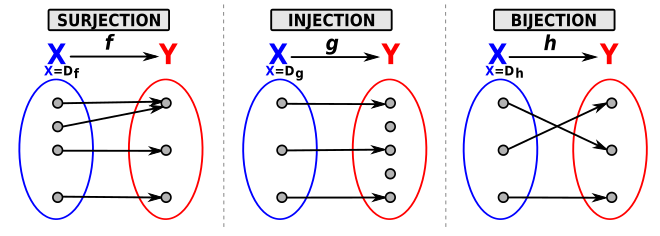
Exemples et contre-exemples

Considérons l'application f : ℝ → ℝ définie par f(x) = 2x + 1. Cette application est injective (et même bijective), puisque pour tous nombres réels arbitraires x et x′, si 2x + 1 = 2x′ + 1 alors 2x = 2x′, soit x = x′.

En revanche, l'application g : ℝ → ℝ définie par g(x) = x2 n'est pas injective, parce que (par exemple) g(1) = 1 = g(−1).

D'autre part, si nous définissons l'application h : ℝ+ → ℝ par la même relation que g,mais avec l'ensemble de définition restreint à l'ensemble des réels positifs, alors l'application h est injective. Une explication est que, pour des réels positifs arbitraires donnés x et x′, si x2 = x′2, alors |x| = |x′|, ainsi x = x′.

Propriétés

Soit f une application de X dans Y.
- f est injective (si et) seulement si X est l'ensemble vide ou s'il existe une application g : Y → X telle que g∘f soit égale à l'application identité sur X, c.-à-d. si et seulement si X est vide ou f est inversible à gauche.
- f est injective si (et seulement si) elle est simplifiable à gauche, c.-à-d. que pour toutes applications g, h : Z → X, f∘g = f∘h entraîne g = h. En d'autres termes, les applications injectives sont précisément les monomorphismes de la catégorie des ensembles.
- Pour toute application g de Y dans Z :
  1. si l'application composée g∘f est injective alors f est injective ;
  2. si f et g sont injectives alors g∘f est injective ;
  3. si f est surjective et si g∘f est injective alors g est injective.
- Les quatre propriétés suivantes sont équivalentes :
  - f est injective ;
  - toute partie A de X est l'image réciproque de son image directe : f−1(f(A)) = A ;
  - pour toutes parties A et B de X, on a f(A ∩ B) = f(A) ∩ f(B) ;
  - pour toute partie A de X, l'image directe du complémentaire de A est incluse dans le complémentaire de l'image directe de A, c.-à-d. f(X\A) ⊂ Y\f(A).
Toute application h : Z → Y peut être décomposée comme h = f∘g pour une injection f et une surjection g convenables. Cette décomposition est unique à un unique isomorphisme près, et f peut être choisie égale à l'injection canonique, de l'image h(Z) de h, dans l'ensemble d'arrivée Y de h.
Si f : X → Y est injective, alors Y a au moins autant d'éléments que X, au sens des cardinaux.
Si l'on note E ≤ F la propriété « il existe une injection de l'ensemble E dans l'ensemble F », alors ≤ est un « préordre » (au sens large, c.-à-d. sur une classe propre : celle de tous les ensembles), qui induit un « ordre » sur la classe des cardinaux. La réflexivité et la transitivité ont été traitées au cours des exemples précédents, et l'antisymétrie est l'objet du théorème de Cantor-Bernstein. Le fait que cet ordre soit total, c'est-à-dire que pour deux ensembles E et F, on a au moins une des relations E ≤ F ou F ≤ E, se démontre à l'aide du lemme de Zorn, c'est le théorème de comparabilité cardinale. Ce résultat est même équivalent à l'axiome du choix.
Un morphisme d'un groupe X dans un groupe Y est injectif si et seulement si son noyau est réduit au sous-groupe trivial du groupe X.

Histoire

Le terme « injection » a été créé par MacLane en 1950 tandis que l'adjectif « injectif » apparaît deux ans plus tard, en 1952, dans les Foundations of Algebraic Topology d'Eilenberg et Steenrod .

Notes et références

Voir par exemple les exercices corrigés du chapitre « Injection, surjection, bijection » sur Wikiversité.
(en) Jeff Miller, « Earliest Known Uses of Some of the Words of Mathematics (I) ».

Portail des mathématiques