Pavage par des polygones réguliers

Pour les articles homonymes, voir Pavage (homonymie).

Cet article traite des pavages par des polygones réguliers.

Dans un pavage du plan euclidien, la somme des angles internes des polygones se rencontrant à un sommet est égale à 360 degrés. Sachant que l'angle interne d'un polygone régulier convexe à n côtés est égal à ${\displaystyle 180\times (1-2/n)}$ degrés, il existe 21 combinaisons possibles de ce type de polygones, dont 11 seulement peuvent conduire à un pavage :

• Avec 3 polygones (les nombres indiquent le nombre de côtés des polygones) :
  • 3 - 7 - 42 : pavage impossible
  • 3 - 8 - 24 : pavage impossible
  • 3 - 9 - 18 : pavage impossible
  • 3 - 10 - 15 : pavage impossible
  • 3 - 12 - 12 : pavage hexagonal tronqué
  • 4 - 5 - 20 : pavage impossible
  • 4 - 6 - 12 : pavage grand rhombitrihexagonal
  • 4 - 8 - 8 : pavage carré tronqué
  • 5 - 5 - 10 : pavage impossible
  • 6 - 6 - 6 : pavage hexagonal

• Avec 4 polygones :
  • 3 - 3 - 4 - 12 : pavage possible, ni régulier, ni semi-régulier
  • 3 - 4 - 3 - 12 : pavage possible, ni régulier, ni semi-régulier
  • 3 - 3 - 6 - 6 : pavage possible, ni régulier, ni semi-régulier
  • 3 - 6 - 3 - 6 : pavage trihexagonal
  • 4 - 4 - 4 - 4 : pavage carré
  • 3 - 4 - 4 - 6 : pavage possible, ni régulier, ni semi-régulier
  • 3 - 4 - 6 - 4 : pavage petit rhombitrihexagonal

• Avec 5 polygones :
  • 3 - 3 - 3 - 3 - 6 : pavage hexagonal adouci
  • 3 - 3 - 3 - 4 - 4: pavage triangulaire allongé
  • 3 - 3 - 4 - 3 - 4: pavage carré adouci

• Avec 6 polygones :
  • 3 - 3 - 3 - 3 - 3 - 3 : pavage triangulaire

Il n'existe pas de pavage du plan avec des polygones réguliers étoilés.

Un pavage est dit régulier s'il consiste en un seul type de polygone régulier. Dans le cas du plan euclidien, il existe trois pavages réguliers^[1] :

• pavage triangulaire, constitué de triangles équilatéraux ;
• pavage carré, constitué de carrés ;
• pavage hexagonal, constitué d'hexagones.

• 
  Pavage triangulaire
• 
  Pavage carré
• 
  Pavage hexagonal

Un pavage est dit semi-régulier s'il est constitué de deux polygones réguliers convexes ou plus, de telle façon qu'un sommet soit toujours entouré des mêmes polygones, dans le même ordre. Dans le cas du plan euclidien, il existe huit pavages semi-réguliers^[2] :

• pavage carré adouci : deux triangles équilatéraux, carré, triangle équilatéral et carré ;
• pavage carré tronqué : carré et deux octogones ;
• pavage hexagonal adouci : quatre triangles équilatéraux et un hexagone ;
• pavage hexagonal tronqué : triangle équilatéral et deux dodécagones ;
• pavage grand rhombitrihexagonal : carré, hexagone et dodécagone ;
• pavage petit rhombitrihexagonal : triangle équilatéral, carré, hexagone et carré ;
• pavage triangulaire allongé : trois triangles équilatéraux et deux carrés ;
• pavage trihexagonal : triangle équilatéral, hexagone, triangle équilatéral et hexagone.

Le pavage hexagonal adouci est chiral : il en existe deux formes distinctes par symétrie. Les autres pavages sont achiraux.

• 
  Pavage hexagonal adouci
• 
  Pavage trihexagonal
• 
  Pavage triangulaire allongé
• 
  Pavage carré adouci
• 
  Pavage petit rhombitrihexagonal
• 
  Pavage carré tronqué
• 
  Pavage hexagonal tronqué
• 
  Pavage grand rhombitrihexagonal

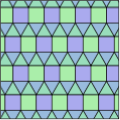
Il est possible de construire des pavages périodiques du plan ni réguliers ni semi-réguliers avec des polygones réguliers convexes. Ces pavages peuvent être classés selon le nombre d'orbites des sommets, arêtes et pavés. Si un pavage comprend n orbites de sommets, il est dit n-uniforme ou n-isogonal ; s'il comprend n orbites d'arêtes, n-isotoxal. Il existe par exemple 20 pavages 2-uniformes, dont 3 exemples sont mentionnés ci-dessous.

• 
  Pavage avec un hexagone et deux triangles
• 
  Pavage avec un dodécagone, trois carrés et douze triangles
• 
  Pavage avec un hexagone, deux carrés et deux triangles

En géométrie hyperbolique, les polygones réguliers ont des angles internes plus petits que leurs équivalent en géométrie euclidienne. Il est possible de réaliser des pavages du plan hyperbolique avec ces polygones^[3].

La galerie ci-dessous affiche quelques exemples de pavages réguliers dans le plan hyperbolique, en utilisant le modèle du disque de Poincaré.

• 
  Pavage triangulaire d'ordre infini
• 
  Pavage carré d'ordre 5
• 
  Pavage pentagonal d'ordre 4
• 
  Pavage grand rhombitrihexagonal d'ordre infini
• 
  Un autre pavage triangulaire d'ordre infini

• (en) Branko Grünbaum et Geoffrey Shephard (trad. du grec ancien), Tilings and Patterns, New York, W. H. Freeman, 1987, 700 p. (ISBN 978-0-7167-1193-3, LCCN 86002007)
• (en) Darrah Chavey, « Tilings by Regular Polygons—II: A Catalog of Tilings », Computers & Mathematics with Applications, vol. 17,‎ 1989, p. 147–165 (DOI 10.1016/0898-1221(89)90156-9)
• (en) Duncan Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover ed. 1958) Chapter X: The Regular Polytopes

• Pavage
• Pavage uniforme (en)
• Polygone régulier

• (en) Uniform Tilings (Steve Dutch, université du Wisconsin à Green Bay)

• Portail de la géométrie