Parallèle (géographie)
La question de Parallèle (géographie) est aujourd’hui très pertinente, car elle touche un large éventail de personnes dans des contextes différents. Tout au long de l’histoire, Parallèle (géographie) a fait l’objet de débats et de controverses, et son impact s’étend à de multiples domaines de la société. C’est pourquoi il est essentiel d’analyser en détail les différentes facettes de Parallèle (géographie), depuis ses origines jusqu’à sa situation actuelle, pour bien comprendre ses implications et trouver des solutions possibles. Dans cet article, nous aborderons différents aspects liés à Parallèle (géographie), offrant une vision complète et exhaustive de ce sujet si d'actualité aujourd'hui.

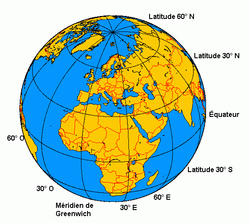
Sur Terre, un parallèle est un cercle abstrait reliant tous les lieux situés sur une même latitude. Leur nom de « parallèles » fait référence au fait qu'ils sont obtenus par intersection de la surface de la Terre avec des plans perpendiculaires à l'axe de rotation de celle-ci[1] et donc parallèles au plan de l'équateur.
Propriétés
Quadrillage
Méridiens et parallèles dessinent un quadrillage sur la surface de la Terre permettant de repérer la position d'un point. Un grand nombre de représentations cartographiques planes sont conçues pour que ce quadrillage soit représenté par deux faisceaux de droites perpendiculaires, les méridiens étant régulièrement espacés, ce qui n'est pas le cas des parallèles. Ce sont les projections dites cylindriques[2].
Propriétés géométriques générales
Les parallèles ont un rayon, et donc un périmètre d'autant plus petit qu'ils se rapprochent d'un pôle et s'éloignent de l'équateur[1].
Comme pour toute surface de révolution, tous les parallèles coupent tous les méridiens à angle droit.
Les parallèles sont des loxodromies, et ne sont donc pas la plus courte distance entre deux points[1].
Cas du modèle sphérique
Si on considère un modèle sphérique, les parallèles associés à des degrés de latitude régulièrement espacés découpent un méridien suivant des longueurs constantes. Ainsi, la distance sur la sphère terrestre[3] d’un degré d'angle est de 111,133 km et celle d'une minute d'angle est de 1 852 m, ce qui correspond au mille marin[4].
Les plans contenant les parallèles, eux, ne sont pas régulièrement espacés et leur distance diminuent de l'équateur au pôle.
Le rayon des parallèles est proportionnel au cosinus de la latitude.
Cas du modèle elliptique
Dans le modèle de l’ellipsoïde, la latitude utilisée est la latitude géodésique, c'est-à-dire l'angle que fait la normale à la surface avec le plan de l'équateur[5].
Dans ce cas, les parallèles associés à des degrés de latitude régulièrement espacés découpent un méridien suivant des longueurs non constantes. Les longueurs sont plus courtes près de l'équateur et plus grandes près du pôle. Ainsi un degré au niveau de l'équateur représente une distance de 110,574 km et à la latitude de la France (46e parallèle), cette distance est de 111,151 km. Au niveau du 75e parallèle, la longueur d'un degré de latitude est portée à 111,618 km[6]. Ces différences de longueur d'arc ont été étudiées au XVIIIe siècle pour valider l'hypothèse d'une terre aplatie aux pôles[7].
 |
 |
| Sphère. Parallèles de latitudes 30° et 60° sur une sphère. Le quart de méridien est découpé en 3 arcs (rouge, bleu et vert) de même longueur. Les plans parallèles ne sont pas équidistants, le rayon des parallèles va en diminuant. | Ellipsoïde. Parallèles de latitudes géodésiques 30° et 60° sur un ellipsoïde . Le quart de méridien est découpé en 3 arcs (rouge, bleu et vert) de longueurs croissantes. Pour mieux saisir le phénomène, l'aplatissement a été amplifié (1/3 au lieu de l'aplatissement réel 1/298[8]). |
Parallèles particuliers
Astronomie

Cinq parallèles ont un rapport avec la rotation de la Terre autour du Soleil :
- le cercle polaire arctique ou cercle arctique (66° 34' N) ;
- le tropique du Cancer (23° 26' N) ;
- l'équateur (0° latitude) ;
- le tropique du Capricorne (23° 26' S) ;
- le cercle polaire antarctique ou cercle antarctique (66° 34' S)[9],[10].
Les deux cercles polaires représentent les limites nord et sud où le Soleil reste au-dessus ou en dessous de l'horizon pendant au moins 24 heures. C'est le lieu où les rayons du soleil sont tangents à la surface aux solstices, à midi ou à minuit.
Les deux tropiques représentent les limites nord et sud où le Soleil peut être vu directement au zénith à midi, au solstice de juin pour l'hémisphère nord et au solstice de décembre pour l'hémisphère sud.
L'équateur représente la ligne d'intersection des deux hémisphères et est le seul parallèle à constituer un grand cercle. Sur cette ligne, aux équinoxes, et à midi solaire, les rayons du Soleil sont perpendiculaires au sol.
Les latitudes des tropiques et des cercles polaires sont liées à l'obliquité, c'est-à-dire l'angle que fait l'axe de rotation de la terre avec la perpendiculaire à l'orbite. Cette obliquité moyenne, qui ne tient pas compte de la nutation, varie au cours des siècles diminuant actuellement d'environ 3/4 de minute par siècle[11]. Elle est, au premier janvier 2025, de 23° 26' 9.745"[12].
Frontières
Lorsque les États se sont constitués, parfois relativement tard parce qu'ils faisaient suite à une colonisation, les frontières furent établies selon des lignes, soit dictées par la géographie (fleuves, montagnes) soit tout simplement par des coordonnées géographiques (méridiens et parallèles). On trouve ces frontières lignes notamment aux États-Unis[13] et en Afrique où 44 % des frontières suivent des méridiens ou des parallèles[14]. On trouve également de telles limitations pour les différents États de l'Australie.
États-Unis
- le 49e parallèle nord : majeure partie de la frontière entre le Canada et les États-Unis ;
- le 45e parallèle nord : frontière entre le Québec et le Vermont ;
- le 42e parallèle nord : frontière entre la Californie et l'Oregon ;
- le 41e parallèle nord : parties des frontières entre le Colorado, le Nebraska, l'Utah et le Wyoming ;
- le 40e parallèle nord : frontière entre le Kansas et le Nebraska ;
- la ligne Mason-Dixon (39° 43' N) : frontière entre le Maryland et la Pennsylvanie ;
- le 37e parallèle nord : frontière entre l'Utah et l'Arizona et entre le Colorado et le Nouveau-Mexique. L'intersection du 109e méridien ouest et du 37e parallèle nord à Four Corners est l'unique point où quatre États se touchent. La frontière nord de l'Oklahoma et la frontière sud du Kansas sont également définies par ce parallèle ;
- le 33e parallèle nord : frontière entre l'Arkansas et la Louisiane.
Afrique
- le parallèle de latitude 27° 40' Nord : frontière entre le Maroc et le Sahara occidental[15] ;
- le 26e parallèle nord : frontière entre la Mauritanie et le Sahara occidental[16] ;
- le 25e parallèle nord : le traité de 1963 place la frontière entre le Mali et la Mauritanie sur ce parallèle pendant 114 miles (183 km)[17] ;
- le 22e parallèle nord : majeure partie de la frontière entre l'Égypte et le Soudan, sur près de 1 200 km[18] ;
- le parallèle de latitude 15°30' : le traité de 1963 place la frontière entre le Mali et la Mauritanie sur ce parallèle pendant 235 miles (378 km)[19] ;
- le 11e parallèle nord : sert de guide de démarcation entre le Burkina Faso et le Ghana[20] ;
- le 1er parallèle nord : frontière entre le Gabon et la Guinée équatoriale[21] ;
- le 1er parallèle sud : frontière entre la Tanzanie et la Gabon sur 232 miles (373 km)[22] ;
- les 7e parallèle et 8e parallèle sud. Dans le traité de 1891, le 8e parallèle servait de démarcation entre l'Angola et le Zaïre de la vallée du Kwango et la rivière Kwilu et le 7e parallèle de la rivière Kwilu à la rivière Kasaï avant que cette frontière ne soit découpée plus finement suivant des vallées et des parallèles (8e, 7°55, 7°34, 7e, 6°55, 7°17)[23] ;
- le 13e parallèle sud : frontière entre l'Angola et la Zambie[24] ;
- le parallèle de latitude 17° 23' 24" Sud : entre les rivières Kunene et Cubango sert de guide au tracé de la frontière entre la Namibie et l'Angola[25], coupant ainsi en deux le royaume de Kwanhama (pt)[26] ;
- le 22e parallèle sud : frontière entre la Namibie et le Botswana[27].
Australie
- le 26e parallèle sud : frontière entre le Territoire du Nord et l'Australie-Méridionale et une partie de la frontière entre le Queensland et l'Australie-Méridionale, entre le 138e méridien est et le 141e méridien est ;
- le 29e parallèle sud : une partie de la frontière entre le Queensland et la Nouvelle-Galles du Sud, en Australie.
Asie
- le 38e parallèle nord : frontière entre les zones d'occupation américaine et soviétique en Corée en 1945 ;
- le 17e parallèle nord : frontière entre la république du Viêt Nam (au sud) et la république démocratique du Viêt Nam (au nord) entre 1954 et 1975.
Divers
- le 60e parallèle sud : frontière nord de l'Antarctique tel que définie dans le traité sur l'Antarctique.
Maritime
Dans le langage maritime, certaines zones particulières possèdent une dénomination spécifique. Dans l'hémisphère sud, on parle des :
- 40es rugissants, pour la zone comprise entre les 40e et 50e parallèles ;
- 50es hurlants, pour la zone comprise entre le 50e parallèle et le 60e parallèle.
Ces zones ont reçu leur nom des grands vents et de la houle quasi omniprésents, dus notamment aux dépressions récurrentes et au courant circumpolaire antarctique ; la zone en devient très dangereuse pour les navires qui y passent.
Notes et références
- « Sphère terrestre », sur Warmaths.
- ↑ Raoul Ibanez, Le rêve de la carte parfaite : Cartographie et Mathématiques, RBA, coll. « Le monde est mathématique », , p. 78-81
- ↑ Supposée conventionnellement d'un double méridien de 40007,863 km.
- ↑ « La terre, coordonnées et cartes », p. 4.
- ↑ « Latitude géodésique », sur AFT.
- ↑ (en) « Length Of A Degree Of Latitude And Longitude Calculator ».
- ↑ Antonio Lafuente et José L. Peset, « La question de la figure de la Terre. L'agonie d'un débat scientifique au XVIIIe siècle », Revue d'histoire des sciences, vol. 37, nos 3-4, , p. 235-254 (lire en ligne)
- ↑ Pierre Causeret, « Il ne faut pas confondre latitude et latitude », Les Cahiers Clairaut, no 98, , p. 2 (245) (lire en ligne)
- ↑ Mise à jour Obliquité
- ↑ Géographie : la rotation de la Terre
- ↑ « Obliquité de la Terre — Astronoo », sur astronoo.com (consulté le ).
- ↑ « Obliquity of the Ecliptic and Nutation », sur neoprogrammics.com (consulté le ).
- ↑ Catherine Coquery-Vidrovitch, « Frontières africaines et mondialisation », Histoire@Politique, no 17, , p. 30 (lire en ligne)
- ↑ Programme Frontières de l'Union Africaine, Délimitation et Démarcation des frontières en Afrique, Commission de l'Union africaine, (lire en ligne), p. 14
- ↑ (en) « Morocco – Western Sahara (Spanish Sahara) Boundary », International Boundary Study, no 9, (lire en ligne), p.3.
- ↑ (en) Ian Brownlie et Ian R. Burns, African Boundaries : A Legal and Diplomatic Encyclopædia, C. Hurst & Co. Publishers, , p. 437.
- ↑ (en) « Mali - Mauritania Boundary », International Boundary Study, no 23, (lire en ligne), p. 6.
- ↑ (en) « Sudan – Egypt (United Arab Republic) Boundary », International Boundary Study, no 18, (lire en ligne).
- ↑ (en) « Mali - Mauritania Boundary », International Boundary Study, no 23, (lire en ligne), p. 3.
- ↑ « Burkina Faso–Ghana Land Boundary », sur Sovereign Limits (consulté le ).
- ↑ « Equatorial Guinea–Gabon Land Boundary », sur Sovereign Limits (consulté le ).
- ↑ (en) « Tanzania – Uganda Boundary », International Boundary Study, no 55, (lire en ligne).
- ↑ (en) « Angola – Democratic Rep. of the Congo (Zaire) Boundary », International Boundary Study, no 144, (lire en ligne).
- ↑ (en) « Angola – Zambia Boundary », International Boundary Study, no 119, (lire en ligne).
- ↑ (en) « Angola – Namibia (South-West Africa) Boundary », International Boundary Study, no 120, (lire en ligne), p. 6.
- ↑ (en) Cristina Udelsmann Rodrigues, « The Kwanhama partitioned by the border and the Angolan perspective of cross-border identity », African Studies, (DOI 10.1080/00020184.2017.132561)
- ↑ (en) Jana Moser, « Border Contracts – Border Conflicts: Examples from Northern Namibia » , sur ICA Commission on the History of Cartography (consulté le ).